递归算法求解n次幂

介绍

LeetCode上面有一个求浮点数的整数次幂的题，题目要求如下

实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，x(n)( )）。

示例 1：

输入：x = 2.00000, n = 10 输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3 输出：9.26100

示例 3：

输入：x = 2.00000, n = -2 输出：0.25000 解释：2(-2) = 1/2(2) = 1/4 = 0.25

实现

递归法的结束点：0次幂或者1的时候要能够求出结果

if(n == 0) {
	return 1;
}
else if(n == 1) {
	return x;
}

如果n是非负数

class Solution {
public:
    double myPow(double x, int n) {
        if(n == 0) {
            return 1;
        }
        else if(n == 1) {
            return x;
        }
        else {
            return x * myPow(x, n-1);
        }
    }
};

如果n是负数

class Solution {
public:
    double myPow(double x, int n) {
        n = -n;
        
        if(n == 0) {
            return 1;
        }
        else if(n == 1) {
            return x;
        }
        
        return 1 / (x * myPow(x, n-1));
    }
};

整合代码（考虑到整数的范围要求）

class Solution {
public:
    double myPow(double x, int n) {
        if(n >= 0) {
            if(n == 0) {
                return 1;
            }
            else if(n == 1) {
                return x;
            }
            else {
                return x * myPow(x, n-1);
            }
        }
        else {
            n = -n;
            return 1 / (x * myPow(x, n-1));
        }
    }
};

总结

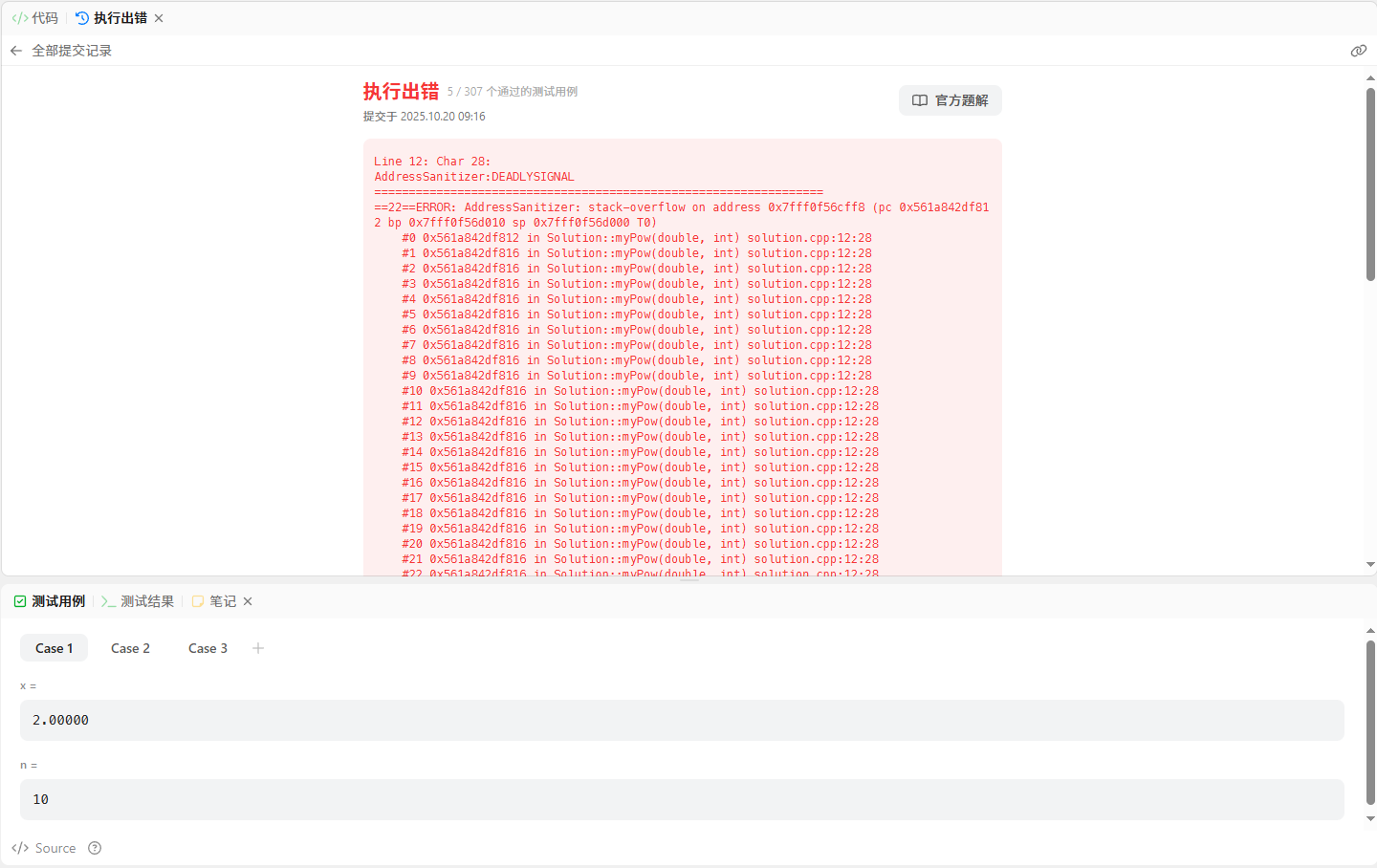
上面3个示例都能正确求解，可见递归法是能够满足题意要求的；但是在实际提交的时候，如果递归的次数过多会造成程序的栈溢出（系统会限制程序栈空间大小，PC端好像是2M还是4M来着，嵌入式就更加敏感）；所以我们一般不整那么多虚的，站在巨人的肩膀上（人生苦短我选std::pow(x,n) ）🙂

本文采用署名-非商业性使用-相同方式共享 4.0 国际许可协议，转载请注明出处。